Question

Find the least number which is a perfect cube and exactly divisible by 6 and 9.

hurry up, I need this answer immediately. ​

Answer 1

Explanation:

216 = 6³ 216/9 = 24 216/6 = 36

Answer 2

To find the least number that is a perfect cube and exactly divisible by 6 and 9, we need to find the least common multiple (LCM) of 6 and 9.

The prime factorization of 6 is
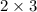`\displaystyle 2 * 3`, and the prime factorization of 9 is
`\displaystyle 3^(2)`.

To find the LCM, we take the highest power of each prime factor that appears in either number. In this case, the highest power of 2 is
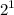`\displaystyle 2^(1)`, and the highest power of 3 is
`\displaystyle 3^(2)`.

Therefore, the LCM of 6 and 9 is
`\displaystyle 2^(1) * 3^(2) =2\cdot 9 =18`.

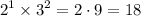Now, we need to find the perfect cube number that is divisible by 18. The smallest perfect cube greater than 18 is
`\displaystyle 2^(3) =8`.

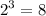However, 8 is not divisible by 18.

The next perfect cube greater than 18 is
`\displaystyle 3^(3) =27`.

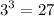Therefore, the least number that is a perfect cube and exactly divisible by both 6 and 9 is 27.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`