Question

A comet follows a hyperbolic path in which the sun is located at one of its foci. If the equation... 100 pts

Answer 1

164 million km

Explanation:

If the hyperbola models the comet's path, and the sun is located at one of its foci, the closest distance the comet reaches to the sun is the distance between a vertex and its corresponding focus.

Therefore, we need to find the vertices and foci of the given hyperbola.

Given equation:

`(x^2)/(60516)-(y^2)/(107584)=1`

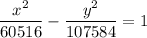
As the x²-term of the given equation is positive, the hyperbola is horizontal (opening left and right).

The general formula for a horizontal hyperbola (opening left and right) is:

`\boxed{\begin{minipage}{7.4 cm}\underline{Standard equation of a horizontal hyperbola}\\\\$((x-h)^2)/(a^2)-((y-k)^2)/(b^2)=1$\\\\where:\\\phantom{ww}$\bullet$ $(h,k)$ is the center.\\ \phantom{ww}$\bullet$ $(h\pm a, k)$ are the vertices.\\\phantom{ww}$\bullet$ $(h\pm c, k)$ are the foci where $c^2=a^2+b^2.$\\\phantom{ww}$\bullet$ $y=\pm (b)/(a)(x-h)+k$ are the asymptotes.\\\end{minipage}}`

Comparing the given equation with the standard equation:

• h = 0
• k = k
• a² = 60516 ⇒ a = 246
• b² = 107584 ⇒ b = 328

To find the loci, we first need to find the value of c:

`\begin{aligned}c^2&=a^2+b^2\\c^2&=60516 +107584\\c^2&=168100\\c&=410\end{aligned}`

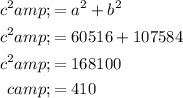
The formula for the loci is (h±c, k). Therefore:

`\begin{aligned}\textsf{Loci}&=(h \pm c, k)\\&=(0 \pm 410, 0)\\&=(-410,0)\;\;\textsf{and}\;\;(410,0)\end{aligned}`

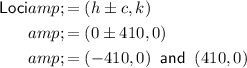
The formula for the vertices is (h±a, k). Therefore:

`\begin{aligned}\textsf{Vertices}&=(h \pm a, k)\\&=(0 \pm 246, 0)\\&=(-246,0)\;\;\textsf{and}\;\;(246,0)\end{aligned}`

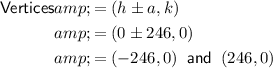
From the given diagram, the vertex and focus have positive x-values. Therefore, the vertex is (246, 0) and the focus is (410, 0).

We need to find the distance between (246, 0) and (410, 0). To do this, simply subtract the x-value of the vertex from the x-value of the focus:

`410-246=164`

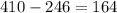
Therefore, the closest distance the comet reaches to the sun is 164 million km.