Question

At what temperature does 1.00 atm of He has have the same density as 1.00 atm of Ne has at 273 K

Answer 1

To find the temperature at which 1.00 atm of He has the same density as 1.00 atm of Ne at 273 K, we can use the ideal gas law and the equation for the density of a gas.

The ideal gas law states that for an ideal gas, the product of its pressure (P) and volume (V) is proportional to the number of moles (n), the gas constant (R), and the temperature (T):

`\displaystyle PV=nRT`

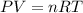
We can rearrange the equation to solve for the temperature:

`\displaystyle T=\frac{{PV}}{{nR}}`

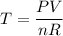
Now let's consider the equation for the density of a gas:

`\displaystyle \text{{Density}}=\frac{{\text{{molar mass}}}}{{RT}}* P`

The density of a gas is given by the ratio of its molar mass (M) to the product of the gas constant (R) and temperature (T), multiplied by the pressure (P).

We can set up the following equation to find the temperature at which the densities of He and Ne are equal:

`\displaystyle \frac{{M_{{\text{{He}}}}}}{{RT_{{\text{{He}}}}}}* P_{{\text{{He}}}}=\frac{{M_{{\text{{Ne}}}}}}{{RT_{{\text{{Ne}}}}}}* P_{{\text{{Ne}}}}`

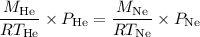
Since we want to find the temperature at which the densities are equal, we can set the pressures to be the same:

`\displaystyle P_{{\text{{He}}}}=P_{{\text{{Ne}}}}`

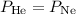
Substituting this into the equation, we get:

`\displaystyle \frac{{M_{{\text{{He}}}}}}{{RT_{{\text{{He}}}}}}=\frac{{M_{{\text{{Ne}}}}}}{{RT_{{\text{{Ne}}}}}}`

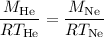
We know that the pressure (P) is 1.00 atm for both gases. Rearranging the equation, we can solve for
`\displaystyle T_{{\text{{He}}}}`:

`\displaystyle T_{{\text{{He}}}}=\frac{{M_{{\text{{Ne}}}}\cdot R\cdot T_{{\text{{Ne}}}}}}{{M_{{\text{{He}}}}}}`

Now we can plug in the molar masses and the given temperature of 273 K for Ne to calculate the temperature at which the densities of He and Ne are equal.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`