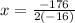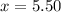Question

The height h(x), of an object is given by the function h(x) = -16x + 176x + 65

where x is time in seconds and h(x) is height in feet. When does the object reach its maximum height? Round your answer to two decimal places.

Answer 1

To find an object's maximum height, we need to find the vertex of this quadratic equation.

Answer: 5.50 seconds

Terms to know:

Quadratic function: A quadratic function is a polynomial function of degree 2, which means the highest power of the variable in the equation is 2.

Vertex: The vertex of a quadratic function is the point on the graph where the function reaches its highest or lowest point. In the case of a quadratic function in the form f(x) = ax^2 + bx + c, the vertex is given by the coordinates (x, f(x)).

Explanation:

The vertex of a quadratic equation can be represented as
`((-b)/(2a), f((-b)/(2a))`

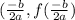
Since we only are looking at the time it takes to reach maximum height we will only look at the x value.

`x= (-176)/(2(-16))`

`x= 5.50`