Question

Ralph chase plans to sell a piece of property for $145000. He wants the money to be paid off in two ways-short term note at 10% interest and a long term note at 8% interest. Find the amount of each note if the total annual interest paid is $13100.

10%:
8%:

Answer 1

100% for the answer

Answer 2

To solve this problem, we can set up a system of equations based on the given information.

Let's assume the amount of money Ralph Chase will receive through the short-term note is represented by "x" and the amount through the long-term note is represented by "y".

According to the problem, the total amount Ralph plans to sell the property for is $145,000. Therefore, we have the equation:

`\displaystyle x+y=145000` ...(1)

Now let's consider the interest paid annually. The interest paid on the short-term note at 10% is calculated as
`\displaystyle 0.10x`, and the interest paid on the long-term note at 8% is
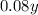`\displaystyle 0.08y`. The total annual interest paid is given as $13,100. Therefore, we have the equation:

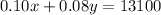`\displaystyle 0.10x+0.08y=13100` ...(2)

We now have a system of two equations (1) and (2). We can solve this system to find the values of "x" and "y".

Multiplying equation (2) by 100 to eliminate decimals, we get:

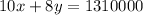`\displaystyle 10x+8y=1310000` ...(3)

Now we can solve equations (1) and (3) simultaneously using any method such as substitution or elimination.

Multiplying equation (1) by 10, we get:

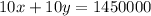`\displaystyle 10x+10y=1450000` ...(4)

Subtracting equation (3) from equation (4), we can eliminate "x" and solve for "y":

`\displaystyle 2y=140000`

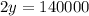
Dividing both sides by 2, we find:

`\displaystyle y=70000`

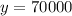
Now substituting the value of "y" back into equation (1), we can solve for "x":

`\displaystyle x+70000=145000`

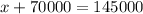
Subtracting 70000 from both sides, we have:

`\displaystyle x=75000`

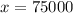
Therefore, the amount of money Ralph Chase will receive through the short-term note is 75,000 and through the long-term note is $70,000.