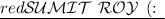Question

What is the freezing point of a solution containing 6.10 grams of benzene (molar mass=78 g/mol) dissolved in 42.0 grams of paradichlorobenzene? The freezing point of pure paradichlorobenzene is 58 degrees celsius and the freezing-point depression constant (Kf) is 7.10 C/m.

Answer 1

To find the freezing point of the solution, we can use the formula for freezing-point depression:

`\displaystyle \Delta T_{\text{f}}=K_{\text{f}} * m`

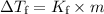
where:

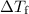`\displaystyle \Delta T_{\text{f}}` is the freezing-point depression,

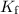`\displaystyle K_{\text{f}}` is the freezing-point depression constant, and

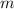`\displaystyle m` is the molality of the solution.

First, we need to calculate the molality of the solution. The molality is defined as the number of moles of solute per kilogram of solvent. In this case, the solvent is paradichlorobenzene.

Step 1: Calculate the number of moles of benzene (solute):

`\displaystyle \text{moles of benzene}=\frac{{\text{mass of benzene}}}{{\text{molar mass of benzene}}}`

`\displaystyle \text{moles of benzene}=\frac{{6.10\, \text{g}}}{{78\, \text{g/mol}}}`

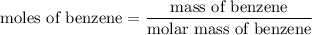
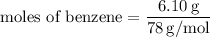
Step 2: Calculate the mass of paradichlorobenzene (solvent):

`\displaystyle \text{mass of paradichlorobenzene}=42.0\, \text{g}`

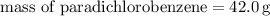
Step 3: Calculate the molality of the solution:

`\displaystyle \text{molality}=\frac{{\text{moles of benzene}}}{{\text{mass of paradichlorobenzene in kg}}}`

`\displaystyle \text{molality}=\frac{{6.10\, \text{g}}}{{42.0\, \text{g}* 0.001\, \text{kg/g}}}`

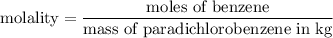
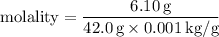
Now that we have the molality, we can calculate the freezing-point depression.

Step 4: Calculate the freezing-point depression:

`\displaystyle \Delta T_{\text{f}}=K_{\text{f}} * \text{molality}`

`\displaystyle \Delta T_{\text{f}}=7.10\, \text{C/m}* \left(\frac{{6.10\, \text{g}}}{{42.0\, \text{g}* 0.001\, \text{kg/g}}}\right)`

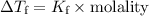
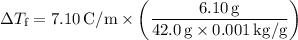
Finally, we can calculate the freezing point of the solution.

Step 5: Calculate the freezing point:

`\displaystyle \text{Freezing point}=58\, \text{C}-\Delta T_{\text{f}}`

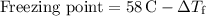
Simplify and compute the values to find the freezing point of the solution.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`