Question

Find the focus of the parabola defined by the equation 100 points.

Answer 1

Answer : Focus is (0,3)

To find the focus of the parabola defined by the equation (y - 3)² = -8(x - 2), we can compare it with the standard form of a parabolic equation: (y - k)² = 4a(x - h).

In the given equation, we have:

(y - 3)² = -8(x - 2)

Comparing it with the standard form, we can determine the values of h, k, and a:

h = 2

k = 3

4a = -8

Solving for a, we get:

4a = -8

a = -8/4

a = -2

Therefore, the vertex of the parabola is (h, k) = (2, 3), and the value of 'a' is -2.

The focus of the parabola can be found using the formula:

F = (h + a, k)

Substituting the values, we get:

F = (2 + (-2), 3)

F = (0, 3)

Therefore, the focus of the parabola defined by the equation (y - 3)² = -8(x - 2) is at the point (0, 3).

Answer 2

Focus = (0, 3)

Explanation:

The focus is a fixed point located inside the curve of the parabola.

To find the focus of the given parabola, we first need to find the vertex (h, k) and the focal length "p".

The standard equation for a sideways parabola is:

`\boxed{(y-k)^2=4p(x-h)}`

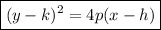
where:

• Vertex = (h, k)
• Focus = (h+p, k)

If p > 0, the parabola opens to the right, and if p < 0, the parabola opens to the left.

Given equation:

`(y-3)^2=-8(x-2)`

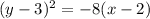
Compare the given equation to the standard equation to determine the values of h, k and p:

• h = 2
• k = 3
• 4p = -8 ⇒ p = -2

The formula for the focus is (h+p, k).

Substituting the values of h, p and k into the formula, we get:

`\begin{aligned}\textsf{Focus}&=(h+p,k)\\&=(2-2,3)\\&=(0,3)\end{aligned}`

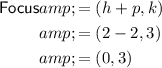
Therefore, the focus of the parabola is (0, 3).