Question

Find the axis of symmetry of the parabola defined by the equation... 100 points

Answer 1

y=2

Explanation:

The equation of a parabola in the form
`(y-k)^2=4p(x-h)` has an axis of symmetry of
`y=k`. Therefore, the axis of symmetry is
`y=2`.

Answer 2

y = 2

Explanation:

The axis of symmetry of a parabola is a line that divides the parabolic curve into two symmetric halves. It is a line of symmetry that passes through the vertex of the parabola.

Given equation of the parabola:

`(y-2)^2=20(x+1)`

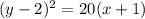
As the y-variable is squared, the given parabola is horizontal (sideways).

The standard form of a sideways parabola is:

`\boxed{(y-k)^2=4p(x-h)}`

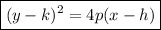
where:

• Vertex = (h, k)
• Focus = (h+p, k)
• Directrix: x = (h - p)
• Axis of symmetry: y = k

Comparing the given equation with the standard equation, we can see that:

• h = -1
• k = 2
• 4p = 20 ⇒ p = 5

As the axis of symmetry is given by the formula y = k, the axis of symmetry of the given parabola is y = 2.