Question

NO LINKS!

Find the standard deviation of the data
9, 16, 23 ,30, 37, 44, 51.

Answer 1

14

Explanation:

To do this on a Ti-84 plus CE

Go to [Stats], click on [1: Edit], and enter {9, 16, 23, 30, 37, 44, 51} into L1

Click on [Stats] again, go to [Calc], and click on [1: 1-Var Stats]

Enter L1 as your List, put nothing for FreqList, and click Calculate

Your
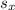`s_(x)` is your standard deviation if your data set is a sample (15.1).

Your σx is your standard deviation if your data set is a population (14).

Answer 2

14

Explanation:

Given data set:

• 9, 16, 23 ,30, 37, 44, 51

To find the standard deviation of a data set, first find the mean (average) of the data, by dividing the sum the data values by the number of data values:

`\begin{aligned}\textsf{Mean}&=(9+16+23+30+37+44+71)/(7)\\\\&=(210)/(7)\\\\&=30\end{aligned}`

Therefore, the mean of the data set is 30.

Calculate the square of the difference between each data point and the mean:

`(9 - 30)^2 = (-21)^2 = 441`

`(16 - 30)^2 = (-14)^2 = 196`

`(23 - 30)^2 = (-7)^2 = 49`

`(30 - 30)^2 = 0^2 = 0`

`(37 - 30)^2 = 7^2 = 49`

`(44 - 30)^2 = 14^2 = 196`

`(51 - 30)^2 = 21^2 = 441`

Find the mean of the squared differences:

`\begin{aligned}\textsf{Mean of squared differences}&=(441+196+49+0+49+196+441)/(7)\\\\&=(1372)/(7)\\\\&=196\end{aligned}`

Finally, square root the mean of the squared differences to get the standard deviation:

`\textsf{Standard deviation}=√(196)=14`

Therefore, the standard deviation of the given data set is 14.