Question

In the map below, Side P Q is parallel to Side S T. Triangle P Q R. Side P Q is 48 kilometers and side P R is 36 kilometers. Triangle S R T. Side R T is 81 kilometers. What is the distance between S and T? If necessary, round to the nearest tenth.

Answer 1

ST = 108km

Explanation:

In ΔPQR and ΔTSR,

∠PRQ = ∠TRS (vertically opposite)

∠PQR = ∠TSR (alternate interior)

∠QPR = ∠ STR (alternate interior)

Since all the angles are equal,

ΔPQR and ΔTSR are similar

Therefore, their corresponding sides have the same ratio

`\implies (ST)/(PQ) = (RT)/(PR)\\ \\\implies (ST)/(48) = (81)/(36)\\\\\implies ST = (81*48)/(36)`

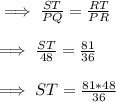
⇒ ST = 108km