Question

An English teacher counted the number of misspelled words in a 1000-word essay he assigned to his students. From a group of 49 students, the mean number of misspelled words was 9.1. The distribution of the student population is normal with a variance of 12.25. What is a confidence interval for the mean number of misspelled words in the student population, considering a confidence level of 99.7%? (Use 3 for the Z value in the formula below)

Answer 1

To calculate the confidence interval for the mean number of misspelled words in the student population, we can use the formula:

Confidence Interval = Mean ± (Z * (Standard Deviation / √(Sample Size)))

Given:
Mean (μ) = 9.1 (mean number of misspelled words)
Sample Size (n) = 49 (number of students)
Variance (σ^2) = 12.25 (variance of the distribution)
Standard Deviation (σ) = √(Variance) = √(12.25) = 3.5
Confidence Level = 99.7% (which corresponds to a Z-value of 3)

Substituting the values into the formula:

Confidence Interval = 9.1 ± (3 * (3.5 / √(49)))

Calculating the expression within the parentheses:

Confidence Interval = 9.1 ± (3 * (3.5 / 7))

Simplifying:

Confidence Interval = 9.1 ± (3 * 0.5)

Confidence Interval = 9.1 ± 1.5

Therefore, the confidence interval for the mean number of misspelled words in the student population, considering a confidence level of 99.7%, is:

Confidence Interval = (9.1 - 1.5, 9.1 + 1.5)
Confidence Interval = (7.6, 10.6)

Answer 2

C. [7.6, 10.6]

Explanation:

To calculate the confidence interval for the mean number of misspelled words in the student population, we can use the confidence interval formula:

`\boxed{CI=\overline{x}\pm z\left((s)/(√(n))\right)}`

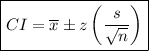
where:

• 
  `\overline{x}` is the sample mean.
• z is the confidence level value.
• s is the sample standard deviation.
• n is the sample size.

Given values:

• 
  `\text{Mean}\;\overline{x} = 9.1`
• 
  `\text{Variance}\;s^2=12.25`
• 
  `\text{Sample size}\;n=49`

The standard deviation is the square root of the variance:

`s=√(s^2)=√(12.25)=3.5`

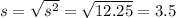
The empirical rule states that approximately 99.7% of the data points will fall within three standard deviations of the mean.

Therefore, z-value for a 99.7% confidence level is z = 3.

Substituting these values into the formula, we get:

`CI=9.1\pm 3\left((3.5)/(√(49))\right)`

`CI=9.1\pm 3\left((3.5)/(7)\right)`

`CI=9.1\pm 3\left(0.5\right)`

`CI=9.1\pm 1.5`

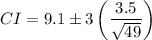
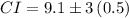
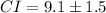
Therefore, the 99.7% confidence limits are:

`CI=9.1-1.5=7.6`

`CI=9.1+1.5=10.6`

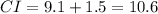
Therefore, the confidence interval for the mean number of misspelled words in the student population is [7.6, 10.6].