Final answer:
The complex number
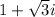 in polar form is
in polar form is
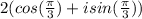 .
.
Step-by-step explanation:
To write the given complex number in polar form, we first need to express the complex number as
z = a + bi,
where
a is the real part and
bi is the imaginary part.
In this case, we have
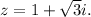
The polar form of a complex number is represented as r(cos(θ) + i sin(θ)),
where
r is the magnitude (modulus) of the complex number and
θ is the argument (angle).
To find r, we calculate the magnitude of the complex number using the formula
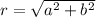
In this case,
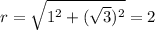 .
.
To find θ, we use the arctangent function (tan^-1(b/a)) to find the angle.
Since a = 1 and
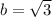
θ
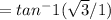 ,
,
which gives us
θ =

So, the polar form of the complex number
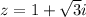 is
is
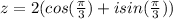 .
.