Question

The expression

28 (78-14)9-13(78-49)9
can be
rewritten as
(X-y)" (262 + y? + gxy). Whatis the value of p?

Answer 1

p =1 0

Explanation:

x³(x - y)⁹ - y³(x - y)⁹ = (x - y)⁹[x³ - y³]

= (x - y)⁹(x - y)(x² + y² + xy)

= (x - y)¹⁰(x² + y² + xy)

where p = 10 and q = 1

Answer 2

p = 10

Explanation:

Given expression:

`x^3(x-y)^9 - y^3(x-y)^9`

Factor out the common term (x - y)⁹:

`(x-y)^9(x^3- y^3)`

`\boxed{\begin{minipage}{5cm}\underline{Difference of two cubes}\\\\$x^3-y^3=(x-y)(x^2+y^2+xy)$\\\end{minipage}}`

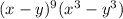
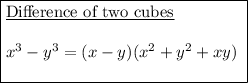
Rewrite the second parentheses as the difference of two cubes.

`(x-y)^9(x-y)(x^2+y^2+xy)`

`\textsf{Apply\:the\:exponent\:rule:} \quad a^b\cdot \:a^c=a^(b+c)`

`(x-y)^(9+1)(x^2+y^2+xy)`

`(x-y)^(10)(x^2+y^2+xy)`

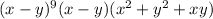
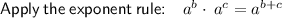
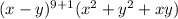
Comparing the rewritten original expression with the given expression:

`(x-y)^(10)(x^2+y^2+xy)=(x-y)^p(x^2+y^2+qxy)`

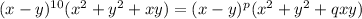
We can see that
`(x-y)^p` corresponds to
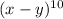`(x-y)^(10)` in the given expression.

Therefore, we can conclude that p = 10.