Question

2 In the diagram below, AOD and COE are straight lines. (a) Find the value of x and y.​

(b) Find the obtuse angle AOC and reflex angle BOE

Answer 1

x = 27.5

y = 21.25

∠AOC = 137.5

∠BOE = 74.5

Explanation:

a)

Since AOD is a straight line ,

∠AOE + ∠EOD = 180

⇒ ∠AOE + 5x= 180

⇒ ∠AOE = 180 - 5x - EQ(1)

∠AOB + ∠BOC + ∠COD = 180

⇒ 32 + 188 - 3x + 2y = 180

⇒ 3x - 2y = 40

⇒ x = (40 + 2y) / 3 - EQ(2)

Since COE is a straight line,

∠EOD + ∠DOC = 180

⇒ 5x + 2y = 180

sub x from eq(2)

5((40 + 2y) / 3) + 2y = 180

`(200 + 10y)/(3) + 2y = 180\\\\(200 + 10y + 6y)/(3) = 180\\\\200 + 16y = 180 *3\\\\16y = 540 - 200\\\\16 y = 340\\\\y = (340)/(16)`

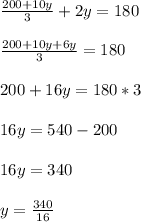
⇒ y = 21.25

sub in eq(2)

x = (40 + 2(21.24)) / 3

`x = (40 + 2(21.25))/(3) \\\\x = (40+42.5)/(3) \\\\x = (82.5)/(3)`

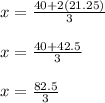
x = 27.5

b) ∠AOC = ∠AOB + ∠BOC

= 32 + 188 - 3x

= 220 - 3(27.5)

= 220 - 82.5

∠AOC = 137.5

From eq(1):

∠AOE = 180 - 5x

= 180 - 5(27.5)

= 180 - 137.5

∠AOE = 42.5

∠BOE = ∠AOB + ∠ AOE

32 + 42.5

∠BOE = 74.5