Question

NO LINKS!! URGENT HELP PLEASE PLEASE!!!​

Answer 1

`\textsf{12)} \quad \text{a.}\;\;m \angle 1 = 107^(\circ), \quad \text{b.}\;\;m \angle 2 = 107^(\circ), \quad \text{c.}\;\;m \angle 3 = 73^(\circ)`

`\textsf{13)} \quad EC = 6`

`\textf{14)}\quad \text{a.}\;\;x = 33, \quad \text{b.}\;\; x = 8`

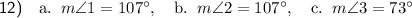
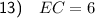
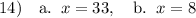
Explanation:

Question 12

As the base angles of an isosceles trapezoid are congruent, the measures of angles E and J are the same. Therefore:

`m\angle 3 = 73^(\circ)`

The opposite angles of an isosceles trapezoid sum to 180°. Therefore:

`\implies m\angle 1 + m\angle 3 = 180^(\circ)`

`\implies m\angle 1 + 73^(\circ) = 180^(\circ)`

`\implies m\angle 1 = 107^(\circ)`

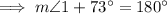
Since the base angles of an isosceles trapezoid are congruent, the measures of angles A and N are the same. Therefore:

`m\angle 2 = 107^(\circ)`

`\hrulefill`

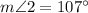
Question 13

The diagonals of isosceles trapezoid ABCD are AC and BD.

Point E is the point of intersection of the diagonals. Therefore:

`BE + ED = BD`

`AE + EC = AC`

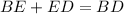
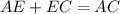
As the diagonals of an isosceles trapezoid are the same length, BD = AC. Therefore:

`AE + EC = BD`

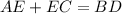
Given BD = 20 and AE = 14:

`\implies AE + EC = BD`

`\implies 14 + EC = 20`

`\implies 14 + EC - 14 = 20 - 14`

`\implies EC = 6`

`\hrulefill`

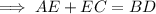
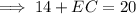
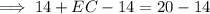
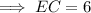
Question 14

The midsegment of a trapezoid is a line segment that connects the midpoints of the two non-parallel sides (legs) of the trapezoid.

The formula for the midsegment of a trapezoid is:

`\boxed{\begin{minipage}{6 cm}\underline{Midsegment of a trapezoid}\\\\$M=(1)/(2)(a+b)$\\\\where:\\ \phantom{ww}$\bullet$ $M$ is the midsegment.\\ \phantom{ww}$\bullet$ $a$ and $b$ are the parallel sides.\\\end{minipage}}`

a) From inspection of the given trapezoid:

• M = x
• a = 18
• b = 48

Substitute these values into the midsegment formula and solve for x:

`x=(1)/(2)(18+48)`

`x=(1)/(2)(66)`

`x=33`

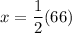
Therefore, the value of x is 33.

b) From inspection of the given trapezoid:

• M = 15
• a = 22
• b = x

Substitute these values into the midsegment formula and solve for x:

`15=(1)/(2)(22+x)`

`30=22+x`

`x=8`

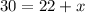
Therefore, the value of x is 8.