Answers:
- (a) 85
- (b)

- (c) Approximately 143.1301 and 216.8699
======================================================
Work shown for part (a)
tan(x) = tan(x-180)
tan(265) = tan(265-180)
tan(265) = tan(85)
-------------------------
Work shown for part (b)
sine = opposite/hypotenuse = 2/3
opposite = 2 and hypotenuse = 3
Use a = 2 and c = 3 to determine b in the pythagorean theorem.
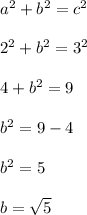
adjacent =
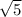 and opposite = 2
and opposite = 2
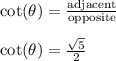
-------------------------
Work shown for part (c)


Here's a table of values for selected inputs of n
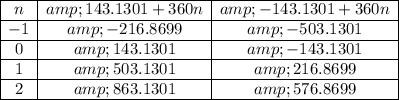
The results 143.1301 and 216.8699 are in the interval
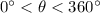 , which makes them the two approximate solutions.
, which makes them the two approximate solutions.
You can use graphing software such as GeoGebra or Desmos to confirm the answers.