Question

NO LINKS!! URGENT HELP PLEASE!!​

Answer 1

`\textsf{a)} \quad \overset{\frown}{AC}=36.65\; \sf inches`

`\textsf{b)} \quad \text{Area of sector $ABC$}=14.14 \; \sf km^2`

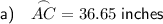
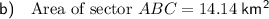
Explanation:

The formula to find the arc length of a sector of a circle when the central angle is measured in degrees is:

`\boxed{\begin{minipage}{6.4 cm}\underline{Arc length}\\\\Arc length $= \pi r\left((\theta)/(180^(\circ))\right)$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius. \\ \phantom{ww}$\bullet$ $\theta$ is the angle measured in degrees.\\\end{minipage}}`

From inspection of the given diagram:

• r = 14 inches
• θ = 150°

Substitute the given values into the formula:

`\begin{aligned}\overset{\frown}{AC}&= \pi (14)\left((150^(\circ))/(180^(\circ))\right)\\\\\overset{\frown}{AC}&= \pi (14)\left((5)/(6)}\right)\\\\\overset{\frown}{AC}&=(35)/(3)\pi\\\\\overset{\frown}{AC}&=36.65\; \sf inches\;(nearest\;hundredth)\end{aligned}`

Therefore, the arc length of AC is 36.65 inches, rounded to the nearest hundredth.

`\hrulefill`

The formula to find the area of a sector of a circle when the central angle is measured in degrees is:

`\boxed{\begin{minipage}{6.4 cm}\underline{Area of a sector}\\\\$A=\left((\theta)/(360^(\circ))\right) \pi r^2$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius. \\ \phantom{ww}$\bullet$ $\theta$ is the angle measured in degrees.\\\end{minipage}}`

From inspection of the given diagram:

• r = 6 km
• θ = 45°

Substitute the given values into the formula:

`\begin{aligned}\text{Area of sector $ABC$}&=\left((45^(\circ))/(360^(\circ))\right) \pi (6)^2\\\\&=\left((1)/(8)\right) \pi (36)\\\\&=(9)/(2)\pi \\\\&=14.14\; \sf km^2\;(nearest\;hundredth)\end{aligned}`

Therefore, the area of sector ABC is 14.14 km², rounded to the nearest hundredth.

Answer 2

a. 36.65 in

b. 14.14 km²

Explanation:

Solution Given:

a.

Arc Length = 2πr(θ/360)

where,

• r is the radius of the circle
• θ is the central angle of the arc

Here Given: θ=150° and r= 14 in

Substituting value

Arc length=2π*14*(150/360) =36.65 in

b.

Area of the sector of a circle = (θ/360°) * πr².

where,

• r is the radius of the circle
• θ is the central angle of the arc

Here θ = 45° and r= 6km

Substituting value

Area of the sector of a circle = (45/360)*π*6²=14.14 km²