Question

You are controlling an unmanned aerial vehicle (UAV) for surveillance. The table shows the height y (in thousands of feet) of the UAV x minutes after you start its descent from cruising altitude.

Answer 1

Answer: y=-1/2x+58, decreases 500, begins, 58k

Explanation:

I'm not too sure about my equation for the word problem but I can explain how I got it.

The equation is in y=mx+b format, so we need to find the slope. They gave us the graph for a reason. You would take each side of the table and subtract/add. For example: 58-53=-5 (y), 0+10=10 (x).

Then, just put that in rise over run (-5/10).

Simplify. Which gives you -1/2.

They already gave us the y-intercept, so just put it into the equation. y=-1/2x+58.

Keep in mind I don't know if you need to add the 0's because it's thousands of feet, I would just in case though. Hoped this helped!

Answer 2

1. An equation for the nth term of the arithmetic sequence is
`a_n = 18n + 26`

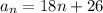
2. A linear function that relates y and x is y = -0.5x + 58.

The slope indicates that the height decreases by 0.5 feet per minute. The y-intercept indicates that the descent begins at a crusing altitude of 58 feet.

In Mathematics and Geometry, the nth term of an arithmetic sequence can be calculated by using this equation:

`a_n=a_1+(n-1)d`

Where:

• d represents the common difference.
• 
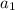  `a_1` represents the first term of an arithmetic sequence.
• n represents the total number of terms.

Part 1.

Next, we would write an explicit equation for the sequence by using the arithmetic sequence formula;

Common difference, d = succeding term - preceeding term

Common difference, d = 62 - 44 = 80 - 62 = 98 - 80

Common difference, d = 18

Hence, an equation that represents this arithmetic sequence is given by;

`a_n=a_1+(n-1)d\\\\a_n=44+(n-1)18\\\\a_n = 18n + 26`

Part 2.

First of all, we would determine the slope;

Slope (m) = (53 - 58)/(10 - 0)

Slope (m) = -0.5

At y-intercept (0, 58) and slope of 0.5, a linear function that relates y and x is given by;

y = -0.5x + 58

In conclusion, the slope indicates that the height decreases by 0.5 feet per minute. The y-intercept indicates that the descent begins at a crusing altitude of 58 feet.