Question

Pls help me with this!! Would be greatly appreciated:).

The function f(t) = 500e^0.04t represents the rate of flow of money in dollars per year. Assume a 10-year period at 5% compounded continuously.
a. Find the present value at t=10.
b. find the accumulated money flow at t=10.

Answer 1

a. To find the present value at t=10, we need to calculate the value of f(t) at t=10. Using the given function f(t) = 500e^(0.04t), we substitute t=10 into the equation:

`\displaystyle \text{Present value} = f(10) = 500e^(0.04(10))`

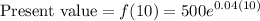
Simplifying the exponent:

`\displaystyle \text{Present value} = 500e^(0.4)`

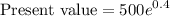
Evaluating the exponent:

`\displaystyle \text{Present value} = 500(2.71828^(0.4))`

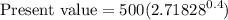
Calculating the value inside the parentheses:

`\displaystyle \text{Present value} = 500(1.49182)`

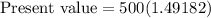
Calculating the product:

`\displaystyle \text{Present value} \approx 745.91`

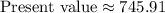
Therefore, the present value at t=10 is approximately $745.91.

b. To find the accumulated money flow at t=10, we need to calculate the integral of f(t) from 0 to 10. Using the given function f(t) = 500e^(0.04t), we integrate the function with respect to t:

`\displaystyle \text{Accumulated money flow} = \int_(0)^(10) 500e^(0.04t) dt`

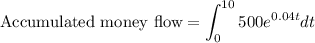
Integrating:

`\displaystyle \text{Accumulated money flow} = 500 \int_(0)^(10) e^(0.04t) dt`

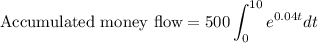
Using the properties of exponential functions, we can evaluate the integral:

`\displaystyle \text{Accumulated money flow} = 500 \left[ \frac{{e^(0.04t)}}{{0.04}} \right]_(0)^(10)`

Simplifying:

`\displaystyle \text{Accumulated money flow} = 500 \left( \frac{{e^(0.4)}}{{0.04}} - \frac{{e^(0)}}{{0.04}} \right)`

Calculating the exponential terms:

`\displaystyle \text{Accumulated money flow} = 500 \left( \frac{{e^(0.4)}}{{0.04}} - \frac{1}{{0.04}} \right)`

Evaluating the exponential term:

`\displaystyle \text{Accumulated money flow} = 500 \left( \frac{{1.49182}}{{0.04}} - \frac{1}{{0.04}} \right)`

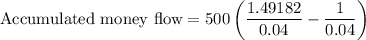
Calculating the subtraction:

`\displaystyle \text{Accumulated money flow} = 500 \left( \frac{{1.49182 - 1}}{{0.04}} \right)`

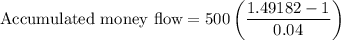
Calculating the division:

`\displaystyle \text{Accumulated money flow} = 500 * 12.2955`

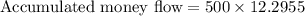
Calculating the product:

`\displaystyle \text{Accumulated money flow} \approx 6147.75`

Therefore, the accumulated money flow at t=10 is approximately $6147.75.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`