Final Answer:
The velocity required for a moving object 5.00×
 m above the surface of Mars to escape from Mars's gravity is approximately 3.66×
m above the surface of Mars to escape from Mars's gravity is approximately 3.66×
 m/s.
m/s.
Step-by-step explanation:
To determine the escape velocity, we can use the escape velocity formula:
![\[ v = \sqrt{(2GM)/(r)} \]](https://img.qammunity.org/2024/formulas/physics/high-school/rzbwzoqmd3db2vhpqiwhyxzht48kjeuvjl.png)
where:
 is the escape velocity,
is the escape velocity,
 is the gravitational constant
is the gravitational constant
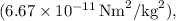
 is the mass of Mars
is the mass of Mars
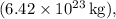
 is the distance from the center of Mars to the object (radius of Mars plus the height above the surface).
is the distance from the center of Mars to the object (radius of Mars plus the height above the surface).
In this case, the radius of Mars
 and the height above the surface
and the height above the surface
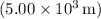 need to be considered. Therefore,
need to be considered. Therefore,
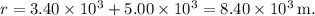
Substituting these values into the formula:
![\[ v = \sqrt{(2 * 6.67 * 10^(-11) * 6.42 * 10^(23))/(8.40 * 10^3)} \]](https://img.qammunity.org/2024/formulas/physics/high-school/63bdkivph1g3k2sk9dl9h1wrd2c5ezj7mp.png)
After evaluating this expression, the escape velocity
 is approximately
is approximately
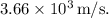
This velocity represents the minimum speed an object must have to escape Mars's gravitational influence and move into space. As an object reaches this velocity, the gravitational pull from Mars is overcome, allowing the object to move freely away from the planet.