Question

Write a rule for the nth term of the geometric sequence and use that rule to find a5
8,56,392

Answer 1

The rule for the nth term of this geometric sequence is an =
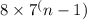`8 * 7^(n-1)`, and the value of the fifth term (a5) is 19,208.

To find the rule for the nth term of a geometric sequence, we need to identify the common ratio (r) between consecutive terms. In this case, we can observe that each term is obtained by multiplying the previous term by 7. Therefore, the common ratio is 7.

The general formula for the nth term of a geometric sequence is given by:

`an = a1 * r^(n-1)`,

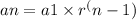where an represents the nth term, a1 is the first term, r is the common ratio, and n is the position of the term.

Using the given sequence, we can determine the value of a1 by examining the first term, which is 8. Plugging in the values into the formula, we have:

`a5 = 8 * 7^(5-1) = 8 * 7^4 = 8 * 7 * 7 * 7 * 7 = 8 * 2401 = 19,208.`

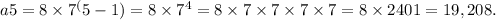
Therefore, the fifth term (a5) in the sequence 8, 56, 392 is 19,208.