Answer:
to solve the equation you first need to bring it to factors and by doing that you first need to let the equation equal 0 hence you need to minus 2 on both sides of the equation therefore
x^2 + 10x + 25 - 2 =2 - 2
therefore
x^2 + 10x +23 = 0
now since the equation cannot be factored, we use the formula.
x=
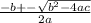
where
a=1
b=10
c=23
note we use the coefficients only.
therefore x =
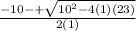
=
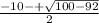
=
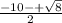
then we form two equations according to negative and positive symbols
x=
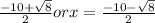
therefore x =
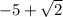 or x=
or x=
