Question

The price of a book is $1 more than twice the price of a ruler. The total price of 5 books and 4 rulers are $47. Find the price of a ruler and a book.​

Answer 1

`\Huge \boxed{\text {Price of a ruler = \$3}}\\\\\\\boxed{\text {Price of a book = \$7}}`

Assigning Variables and Creating Formulas

Let's start by setting up some equations based on the given information.

Let's call the price of a ruler "
`r`" and the price of a book "
`b`".

From the first sentence, we know that:

`b = 2r + 1`

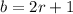
From the second sentence, we know that the total price of 5 books and 4 rulers is $47. We can express this as an equation:

`5b + 4r = 47`

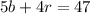
Price of a Ruler

Now we can substitute the first equation into the second equation to eliminate "
`b`" and get an equation in terms of "
`r`" only:

`5(2r + 1) + 4r = 47`

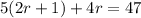
Simplifying this, we get:

`\boxed{\begin{minipage}{7 cm}$\Rightarrow$ 10r + 5 + 4r = 47 \\ \\$\Rightarrow$ 14r + 5 = 47 \\ \\$\Rightarrow$ 14r = 42 \\ \\$\Rightarrow$ r = 3\end{minipage}}`

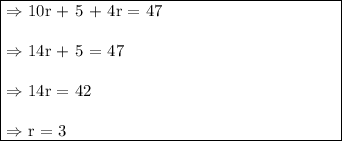
So the price of a ruler is $3.

Price of a Book

To find the price of a book, we can use the first equation:

`\boxed{\begin{minipage}{7 cm} \text{\LARGE b = 2r + 1} \\ \\$\Rightarrow$ b = 2(3) + 1 \\ \\$\Rightarrow$ b = 6 + 1 \\ \\$\Rightarrow$ b= 7\end{minipage}}`

So the price of a book is $7.

Therefore, the price of a ruler is $3 and the price of a book is $7.

_______________________________________________________

Answer 2

book = $7

ruler = $3

Explanation:

Let the price of a book be b and the price of a ruler be r

b = 1 + 2r ---eq(1)

5b + 4r = 47 ---eq(2)

sub eq(1) in eq(2),

5(1 + 2r) + 4r = 47

⇒ 5 + 10r + 4r = 47

⇒ 14r = 42

⇒r = 3

sub r in eq(1)

b = 1 + 2(3)

⇒ b = 7