Answer:
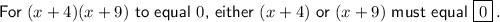
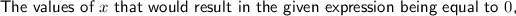

Explanation:
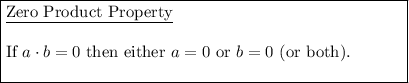
According to the Zero Product Property, for (x + 4)(x + 9) to equal zero, then either (x + 4) or (x + 9) must equal zero.
Set each factor equal to zero and solve for x:
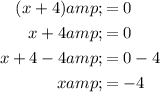
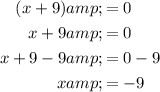
Therefore, the values of x that would result in the given expression being equal to zero, in order from least to greatest, are -9 and -4.