Question

An electron is in the hydrogen atom with n = 3. For related problem-solving tips and strategies, you may want to view a Video Tutor Solution of Angular momentum states. Part C For each value of L, find all the possible angles between I and the z axis. Express your answers in degrees in ascending order separated by commas. IVE ΑΣΦ ^ C ? For L = √2h: 0= Submit Request Answer Part D Express your answers in degrees in ascending order separated commas. -- ΑΣΦ ? For L = √6ħ0- Submit Provide Feedback Request Answer Next >

Answer 1

The possible angles between L and the z-axis for L = √6ħ are:

-90°, -54.7°, -30°, -18.4°, 18.4°, 30°, 54.7°, 90° (in ascending order). To find the possible angles between the angular momentum vector (L) and the z-axis for a given value of L, we can use the equation:

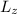`L_z`= mħ

where
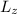`L_z` is the z-component of the angular momentum, m is the magnetic quantum number, and ħ is the reduced Planck's constant.

In the case of hydrogen atom with n = 3, the possible values of L can be found using the relation:

L = √(L(L + 1))ħ

where L is the total orbital angular momentum quantum number.

Let's calculate the angles for each given value of L:

Part C: For L = √2ħ

Using the equation L = √(L(L + 1))ħ, we have:

√2ħ = √(L(L + 1))ħ

Simplifying the equation, we find:

2 = L(L + 1)

This is a quadratic equation, which can be solved to find the possible values of L. In this case, the solutions are:

L = 1, -2

To find the possible angles between L and the z-axis, we use the values of m, which range from -L to +L. Therefore, for L = 1, the possible values of m are -1, 0, and 1.

Using the equation Lz = mħ, we can calculate the angles θ:

For m = -1: Lz = -ħ

For m = 0: Lz = 0

For m = 1: Lz = ħ

So, the possible angles between L and the z-axis for L = √2ħ are:

-180°, 0°, 180° (in ascending order)

Part D: For L = √6ħ

Using the equation L = √(L(L + 1))ħ, we have:

√6ħ = √(L(L + 1))ħ

Simplifying the equation, we find:

6 = L(L + 1)

Solving the quadratic equation, we get:

L = 2, -3

For L = 2, the possible values of m range from -2 to +2.

For L = -3, the possible values of m range from -3 to +3.

Using the equation
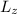`L_z` = mħ, we can calculate the angles θ:

For L = 2, the possible angles between L and the z-axis are:

-90°, -30°, 30°, 90°

For L = -3, the possible angles between L and the z-axis are:

-90°, -54.7°, -18.4°, 18.4°, 54.7°, 90°