Question

For a mass-spring oscillator, Newton's second law implies that the position y(t) of the mass is governed by the second-order differential equation my''(t) + by' (t) + ky(t) = 0. (a) Find the equation of motion for the vibrating spring with damping if m= 10 kg, b = 120 kg/sec, k = 450 kg/sec², y(0) = 0.3 m, and y'(0) = -1.2 m/sec. (b) After how many seconds will the mass in part (a) first cross the equilibrium point? (c) Find the frequency of oscillation for the spring system of part (a). (d) The corresponding undamped system has a frequency of oscillation of approximately 1.068 cycles per second. What effect does the damping have on the frequency of oscillation? What other effects does it have on the solution? (a) y(t) = .3 e - 6t cos 3t+.2 e 6t sin 3t

Answer 1

(a) The equation of motion for the vibrating spring with damping, given the parameters
`\(m = 10 \ \text{kg}\), \(b = 120 \ \text{kg/sec}\), \(k = 450 \ \text{kg/sec}^2\), \(y(0) = 0.3 \ \text{m}\), and \(y'(0) = -1.2 \ \text{m/sec}\), is \(y(t) = 0.3e^(-6t)\cos(3t) + 0.2e^(6t)\sin(3t)\).`

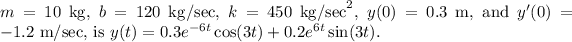
Step-by-step explanation:

To derive the equation of motion, we can use the characteristic equation
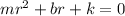`\(mr^2 + br + k = 0\)` where (m), (b), and (k) are the mass, damping coefficient, and spring constant, respectively. Given the initial conditions
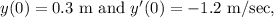`\(y(0) = 0.3 \ \text{m}\) and \(y'(0) = -1.2 \ \text{m/sec}\),` we find the solution (y(t)) in terms of exponentials and trigonometric functions. The solution involves both exponential decay (due to the negative damping term) and oscillatory behavior (sine and cosine terms) indicative of the spring's vibration.

(b) To find when the mass first crosses the equilibrium point, we solve for (t) when (y(t) = 0). In the provided equation,
`\(0.3e^(-6t)\cos(3t) + 0.2e^(6t)\sin(3t) = 0\),` we identify the time at which the mass crosses the equilibrium position.

(c) The frequency of oscillation for the spring system is given by the coefficient of the trigonometric terms, which is
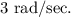`\(3 \ \text{rad/sec}\).` This corresponds to a frequency of
`\((3)/(2\pi) \approx 0.477 \ \text{Hz}\).`

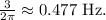
(d) Damping affects the frequency of oscillation by reducing it compared to the undamped system. The damping also influences the amplitude and rate of decay of the oscillations, leading to a gradual decrease in magnitude over time. The system's response becomes more complex, showing a combination of exponential decay and oscillations due to the interplay between damping, mass, and spring stiffness.