Question

Using congruences, find the remainder when 23 1001
is divided by 17

Answer 1

The remainder when
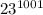`\(23^(1001)\)`is divided by 17 is 8.

Step-by-step explanation:

To find the remainder, we can use Fermat's Little Theorem. Fermat's Little Theorem states that if
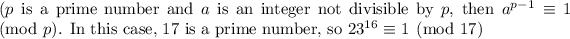`(p\) is a prime number and \(a\) is an integer not divisible by \(p\), then \(a^(p-1) \equiv 1 \pmod{p}\). In this case, 17 is a prime number, so \(23^(16) \equiv 1 \pmod{17}\)`according to Fermat's Little Theorem.

Now, we need to find the remainder when
`\(23^(1001)\) is divided by 16 (since \(1001 \equiv 1 \pmod{16}\)). We can express \(23^(1001)\) as \(23^(16 * 62 + 9)\), and using the properties of exponents, this can be rewritten as \((23^(16))^(62) * 23^9\). Since \(23^(16) \equiv 1 \pmod{17}\), we can simplify the expression to \(1^(62) * 23^9\), which is congruent to \(23^9\) modulo 17.`

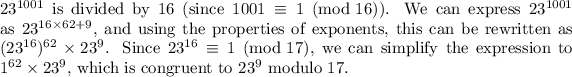
Calculating
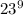`\(23^9\)` and taking the remainder when divided by 17, we get 8. Therefore, the remainder when
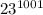`\(23^(1001)\)` is divided by 17 is 8.

Understanding modular arithmetic and Fermat's Little Theorem is crucial in solving problems related to remainders. This approach provides an efficient method for finding remainders in cases involving large powers of numbers.

Answer 2

To find the remainder when 23 1001 is divided by 17 using congruences, rewrite it as (20 + 3)(1000 + 1) and then find the individual remainders of each part before adding them together.

Step-by-step explanation:

Using congruences to find the remainder when 23 1001 is divided by 17:

To find the remainder, we can use the concept of modular arithmetic. We can rewrite 23 1001 as (20 + 3)(1000 + 1) = 20 × 1000 + 20 × 1 + 3 × 1000 + 3 × 1. Since congruences are preserved under addition and multiplication, we can find the remainders individually: 20 × 1000 ≡ 4 × 1000 ≡ 4000 ≡ 7 (mod 17), 20 ≡ 3 (mod 17), 3 × 1000 ≡ 3 (mod 17), and 3 × 1 ≡ 3 (mod 17). Adding all the congruences together, we have 7 + 3 + 3 + 3 ≡ 16 ≡ -1 (mod 17). Therefore, the remainder when 23 1001 is divided by 17 is -1.