Question

Given \( y: \mathbb{Z} \rightarrow \mathbb{Z} \) with \( y(\beta)=\frac{-\beta^{2}}{-4+\beta^{2}} \). With justification, show that \( y(\beta) \) is not one-to-one, not onto and not bijective. [10 ma

Answer 1

Given
`\sf y: \mathbb{Z} \rightarrow \mathbb{Z}` with
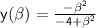`\sf y(\beta)=(-\beta^(2))/(-4+\beta^(2))`. We need to show that
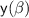`\sf y(\beta)` is not one-to-one, not onto, and not bijective.

To show that
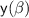`\sf y(\beta)` is not one-to-one, we need to demonstrate that there exist two distinct elements
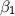`\sf \beta_1` and
`\sf \beta_2` in the domain
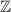`\sf \mathbb{Z}` such that
`\sf y(\beta_1) = y(\beta_2)`.

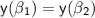Let's consider
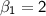`\sf \beta_1 = 2` and
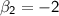`\sf \beta_2 = -2`. Plugging these values into the equation for
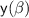`\sf y(\beta)`, we have:

`\sf y(\beta_1) = (-2^2)/(-4+2^2) = (-4)/(0)`

`\sf y(\beta_2) = (-(-2)^2)/(-4+(-2)^2) = (-4)/(0)`

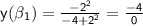
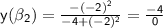
Since both
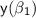`\sf y(\beta_1)` and
`\sf y(\beta_2)` evaluate to
`\sf (-4)/(0)`, we can conclude that
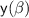`\sf y(\beta)` is not one-to-one.

Next, to show that
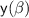`\sf y(\beta)` is not onto, we need to find an element
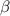`\sf \beta` in the domain
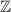`\sf \mathbb{Z}` for which there is no corresponding element
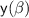`\sf y(\beta)` in the codomain
`\sf \mathbb{Z}`.

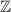Let's consider
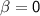`\sf \beta = 0`. Plugging this value into the equation for
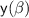`\sf y(\beta)`, we have:

`\sf y(0) = (0^2)/(-4+0^2) = (0)/(-4)`

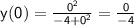
Since the denominator is non-zero, we can see that
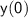`\sf y(0)` is undefined. Therefore, there is no corresponding element in the codomain
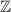`\sf \mathbb{Z}` for
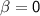`\sf \beta = 0`, indicating that
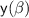`\sf y(\beta)` is not onto.

Finally, since
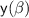`\sf y(\beta)` is neither one-to-one nor onto, it is not bijective.

Hence, we have shown with justification that
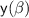`\sf y(\beta)` is not one-to-one, not onto, and not bijective.