Question

NO LINKS!! URGENT HELP PLEASE!!​

Answer 1

Answer: 12, 30, 162

Explanation:

b) For a regular polygon the central angles will all add up to 360

n= number of sides = 360/30

n=12

d) For exterior angles, the sum of the exterior angles is also 360

n = number of sides = 360/12

n=30

f) for any polygon

interior ange = ((n-2)180) / n

interior angle = ((20-2)180 / 20

interior angle = (18)(180) / 20

interior angle = 162

Answer 2

b. 12

d. 30

f. 162°

Explanation:

b. The number of sides of a regular polygon can be found by dividing 360° by the central angle.

In this case, the central angle is 30°, so the number of sides is 360° / 30° = 12.

The polygon is a dodecagon.

d. The number of sides of a regular polygon can be found by dividing 360° by the exterior angle.

In this case, the exterior angle is 12°, so the number of sides is 360° / 12° = 30.

The polygon is a triacontagon.

f. The interior angle of a regular polygon can be found by using the formula
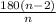`(180(n-2) )/(n)`where n is the number of sides.

In this case, n=20, so the interior angle is 180(20-2) / 20 = 162°.