Question

NO LINKS! URGENT HELP PLEASE!

Find the surface area. Leave answers exact ​

Answer 1

Explanation:

b) Flip on its side so the triangle is the base

SA = Ph + 2B

P = perimeter of base

P = 8+6+hypotenuse

hypotenuse² =8²+6²

hypotenuse² = 100

hypotenuse = 10

P = 8+6+10

P= 24

h=height=5

B = area of base

B= 1/2 bh

B= 1/2 (8)(6)

B= 24

SA = Ph + 2B

SA = (24)(5) + 2(24)

SA = 168 yd²

d) SA (sphere) = 4
`\pi`r²

r=12

SA = 4
`\pi`(12)²

SA = 576
`\pi` yd²

Answer 2

b) 158 yd²

d) 576π yd²

Explanation:

Part b

The surface area of a triangular prism is made up of 2 congruent triangles and 3 rectangles.

The area of a triangle is half the product of its base and height.

The area of a rectangle is the product of its width and length.

Therefore, to calculate the surface area of the given triangular prism, we first need to find the length of the hypotenuse (H) of the triangular base. To do this, we can use Pythagoras Theorem:

`\begin{aligned}H^2&=6^2+8^2\\H^2&=36+84\\H^2&=100\\H&=√(100)\\H&=10\; \sf yd\end{aligned}`

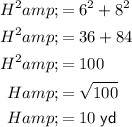
Therefore, the surface area of the given triangular prism is:

`\begin{aligned}\textsf{Surface Area}&=2 \cdot \left((1)/(2) \cdot 6 \cdot 8\right)+(6 \cdot 5)+(8 \cdot 5)+(10 \cdot 5)\\\\&=2 \cdot \left(24)+30+40+50\\\\&=48+30+40+50\\\\&=158\; \sf yd^2\end{aligned}`

`\hrulefill`

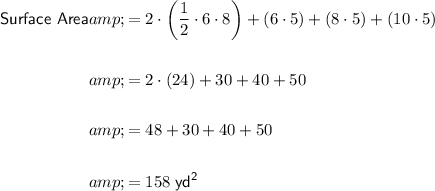
Part d

The formula for the surface area of a sphere is:

`\boxed{\begin{minipage}{4 cm}\underline{Surface area of a sphere}\\\\$SA=4 \pi r^2$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius.\\\end{minipage}}`

From the given diagram, the diameter of the sphere is 24 yd.

As the diameter is twice the radius, the radius of the sphere is r = 12.

Substitute the value of r into the formula to calculate the surface area of the sphere:

`\begin{aligned}\textsf{Surface area}&=4 \pi (12)^2\\&=4 \pi (144)\\&=576\pi \; \sf yd^2\end{aligned}`

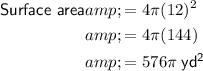
Therefore, the surface area of the sphere is 576π yd².