Answer: 40
Step-by-step explanation:
To answer this question, it is important to think about the ratio of cars:trucks
we know that 20% of all the vehicles are trucks
which means that 80% of all the vehicles must be cars
this means that the ratio of cars to trucks is 80%:20%
- you may drop the percent and simplify the fraction to 4:1 at this point
---- 80/20 = 8/2 = 4/1 (just to show where that fraction came from)
so now we know:
ratio of cars to trucks = 4:1
cars = 30 + trucks
now you can set up an equation to solve for the missing information
 =
=
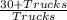 --> where we have listed cars simply as 30 + trucks to only have one variable in the equation
--> where we have listed cars simply as 30 + trucks to only have one variable in the equation
from here you can simplify the fraction
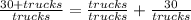
at this point you will see that
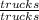 can simplify to 1
can simplify to 1
so now you have
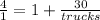
at this point, simplify 4/1 to just 4
4 = 1 +
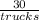
subtract 1 from both sides
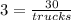
now you can write
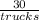 as
as
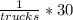
from here, divide both sides by 30 to get
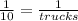
since these fractions must be equal, we now know that there must be 10 trucks
using 30 + trucks = cars --> we know that there are 40 cars
let's check using the other given info
if there are 10 trucks and 40 cars = 50 vehicles total
20% of 50 = 10 ; which proves that 20% of all vehicles in the lot are trucks and we have the right answer
ANSWER: there are 40 Cars in the parking lot