Question

Write slope intercept form

Answer 1

keeping in mind that perpendicular lines have negative reciprocal slopes, let's check for the slope of the equation above

`y=\stackrel{\stackrel{m}{\downarrow }}{-\cfrac{2}{3}}x+3\qquad \impliedby \qquad \begin{array}c \cline{1-1} slope-intercept~form\\ \cline{1-1} \\ y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}} \\\\ \cline{1-1} \end{array} \\\\[-0.35em] ~\dotfill`

`\stackrel{~\hspace{5em}\textit{perpendicular lines have \underline{negative reciprocal} slopes}~\hspace{5em}} {\stackrel{slope}{ \cfrac{-2}{7}} ~\hfill \stackrel{reciprocal}{\cfrac{7}{-2}} ~\hfill \stackrel{negative~reciprocal}{-\cfrac{7}{-2} \implies \cfrac{7}{ 2 }}}`

so we're really looking for the equation of a line whose slope is 7/2 and it passes through (-2 , -2)

`(\stackrel{x_1}{-2}~,~\stackrel{y_1}{-2})\hspace{10em} \stackrel{slope}{m} ~=~ \cfrac{7}{2} \\\\\\ \begin{array} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-2)}=\stackrel{m}{ \cfrac{7}{2}}(x-\stackrel{x_1}{(-2)}) \implies y +2 = \cfrac{7}{2} ( x +2) \\\\\\ y+2=\cfrac{7}{2}x+7\implies {\Large \begin{array}{llll} y=\cfrac{7}{2}x+5 \end{array}}`

Answer 2

Answer: y =
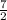`(7)/(2)`x + 5

Explanation:

Slope-intercept form is written in the form of y = mx + b.

Perpendicular lines have slopes that are the opposite of the reciprocals of each other. This means that if the perpendicular line has a slope of
`-(2)/(7)`, our line will have a slope of
`(7)/(2)`.

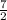Lastly, we can substitute this into a y = mx + b equation as m (the slope) and solve for b (the y-intercept) using the point given.

y = mx + b

y =
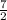`(7)/(2)`x + b

(-2) =
`(7)/(2)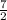`(-2) + b

-2 = -7 + b

b = 5

I have graphed the given line and y =
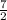`(7)/(2)`x + 5. You can see that these two lines are perpendicular.