Question

Use trigonometry to solve for the missing angle.

Answer 1

71.8962°

Explanation:

In order to find the angle given 2 sides, you need to identify the 2 sides with the given measure.

Since we need to find X, the 2 sides are 52 (the opposite side) and 17 (the adjacent side)

The only way to find X with an opposite and adjacent side is by using tan.

In order to find the angle, you will need to use the tan^-1 (52/17)

That will give you 71.8962°

Answer 2

x = 71.9°

Explanation:

The given diagram shows a right triangle with an unknown angle, x.

We have been given the measures of the sides that are opposite and adjacent the unknown angle. Therefore, we can use the tangent trigonometric ratio to find the value of x.

`\boxed{\begin{minipage}{7 cm}\underline{Tangent trigonometric ratio} \\\\$\sf \tan(\theta)=(O)/(A)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle.\\\end{minipage}}`

The unknown angle is x, so θ = x.

The side opposite the angle measures 52 units, so O = 52.

The side adjacent the angle measures 17 units, so A = 17.

Substitute the values into the ratio and solve for x:

`\tan x=(52)/(17)`

`x=\tan^(-1)\left((52)/(17)\right)`

`x=71.8962369...`

`x=71.9^(\circ)\; \sf (nearest\;tenth)`

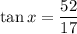
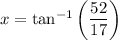
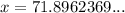
Therefore, the value of x is 71.9°.