Question

Find the solution of the following initial value problem. y" + 8y + 15y = 0 y(0) = 10, y'(0) = -36 NOTE: Use t as the independent variable. y(t) =

Answer 1

`y(t)=7e^(-3t)+3e^(-5t)`

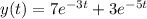
Explanation:

Solve the given initial-value problem.

`y`

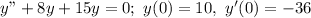
(1) - Form and solve the characteristic equation for "m"

`y`

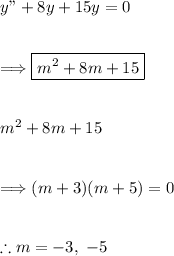
(2) - Form the general solution

`\boxed{\left\begin{array}{ccc}\text{\underline{Solutions to Higher-order DE's:}}\\\\\text{Real,distinct roots} \rightarrow y=c_1e^(m_1t)+c_2e^(m_2t)+...+c_ne^(m_nt)\\\\ \text{Duplicate roots} \rightarrow y=c_1e^(mt)+c_2te^(mt)+...+c_nt^ne^(mt)\\\\ \text{Complex roots} \rightarrow y=c_1e^(\alpha t)\cos(\beta t)+c_2e^(\alpha t)\sin(\beta t)+... \ ;m=\alpha \pm \beta i\end{array}\right}`

The roots are real and distinct, so we can form the general solution as:

`\therefore y=c_1e^(-3t)+c_2e^(-5t)`

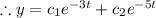
(3) - Now use the given initial conditions to determine the values for the arbitrary constants c_1 and c_2

`y=c_1e^(-3t)+c_2e^(-5t); \ \text{Recall} \rightarrow \ y(0) = 10, \ y'(0) = -36\\\\\\y=c_1e^(-3t)+c_2e^(-5t)\\\\y'=-3c_1e^(-3t)-5c_2e^(-5t)\\\\\text{Plugging in the initial conditions:}\\ \Longrightarrow \left\{\begin{array}{cc}10=c_1+c_2\\-36=-3c_1-5c_2\end{array}\right\\\\\\\text{After solving the system we get:} \ \boxed{c_1=7, \ c_2=3}`

(4) - Now we can form the solution

`\therefore \boxed{\boxed{y(t)=7e^(-3t)+3e^(-5t)}}`