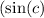Question

For approximately what values of x can you replace sin(x) by x−(x3/6) with an error of magnitude no greater than 4∗10−3 ?

Answer 1

To replace sin(x) by x - (x^3/6) with an error no greater than 4∗10^-3, the values of x that satisfy the condition are approximately -0.029 ≤ x ≤ 0.029.

Step-by-step explanation:

To replace sin(x) by x - (x^3/6) with an error no greater than 4∗10^-3, we need to find the values of x for which the absolute value of the difference between the two functions is less than or equal to 4∗10^-3.

Using the inequality |sin(x) - (x - (x^3/6))| ≤ 4∗10^-3, we can simplify it to |x^3/6| ≤ 4∗10^-3.

By solving the inequality, we find that the values of x that satisfy the condition are approximately -0.029 ≤ x ≤ 0.029.

Answer 2

You can replace
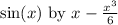`\(\sin(x)\) by \(x - (x^3)/(6)\)` with an error of magnitude no greater than
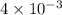`\(4 * 10^(-3)\)` for values of x within the range [-1.1, 1.1].

Step-by-step explanation:

The question involves Taylor series and understanding the approximation of
`\(\sin(x)\)`by its Taylor series expansion. The Taylor series expansion for
`\(\sin(x)\)` up to the third-degree term is given by
`\(\sin(x) \approx x - (x^3)/(6)\).`

To determine the range of x values for a given error threshold, we can consider the remainder term in the Taylor series, which is proportional to the fourth derivative of \(\sin(x)\). The remainder term can be expressed using the Lagrange form of the remainder,
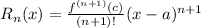`\(R_n(x) = (f^((n+1))(c))/((n+1)!)(x-a)^(n+1)\)`, where \(c\) is between \(a\) and \(x\).

For the given error threshold
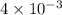`\(4 * 10^(-3)\)`, we can set up the inequality
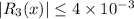`\(|R_3(x)| \leq 4 * 10^(-3)\)`and solve for x. In the case of
`\(\sin(x)\)`, the fourth derivative is
`\(\sin(x)\)`, so
`\(|R_3(x)| = (|\sin(c)|)/(24)|x|^4\).`

Solving the inequality involves finding the maximum absolute value of
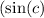`(\sin(c)\)`within the range [-1,1] and this occurs when
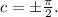`\(c = \pm (\pi)/(2)\).`Thus, the range for x is determined by
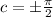`\(c = \pm (\pi)/(2)\)`. leading to
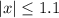`\(|x| \leq 1.1\)`.
`(\sin(c)\)`