Question

Word problem about related rates, 30 points.

Answer 1

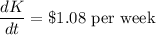`(dK)/(dt)= \$ 1.08 \ \text{per week}`, the capital investment is decreasing.

Explanation:

To find the rate at which capital investment is changing when output is kept constant, we need to differentiate the output function with respect to time, t, and solve for the rate of change of capital investment, dK/dt.

The given output function is:

`Q = 90K^(2/3)L^(1/3)`

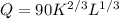
To find the rate of change, we differentiate both sides of the equation with respect to time. First rearrange the equation.

`Q = 90K^(2/3)L^(1/3)\\\\\\\Longrightarrow K^(2/3)=(Q)/(90L^(1/3))`

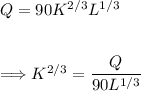
Now differentiating...

`K^(2/3)=(Q)/(90L^(1/3))\\\\\\\Longrightarrow 2/3 * K^(-1/3) * (dK)/(dt) = (Q)/(90L^(4/3)) * -1/3 * (dL)/(dt) \\\\\\\therefore \boxed{(dK)/(dt)=-(Q)/(180L^(4/3)K^(-1/3)) * (dL)/(dt)}`

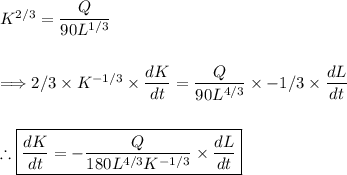
Substitute in all our given values...

`(dK)/(dt)=-(Q)/(180L^(4/3)K^(-1/3)) * (dL)/(dt)\\\\\\\Longrightarrow (dK)/(dt)=-(90K^(2/3)L^(1/3))/(180L^(4/3)K^(-1/3)) * (dL)/(dt)\\\\\\\Longrightarrow (dK)/(dt)=-(K)/(2L) * (dL)/(dt)\\\\\\\Longrightarrow (dK)/(dt)=-(27)/(2(1000)) * 80\\\\\\ \therefore\boxed{\boxed{(dK)/(dt)=-(27)/(25)\approx -1.08}}`

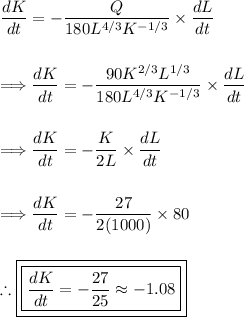
Thus, the capital investment is decreasing at a rate of $1.08 per week.