Question

Find the equation of the tangent to y = x^4 – x^2 at the point where x=1.

Does the tangent intersect the curve again?

Answer 1

`y=2x-2`

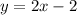
Explanation:

The equation of the tangent line can be found by using the formula
`y-y_1=m(x-x_1)` where
`m` is the slope and
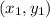`(x_1,y_1)` are the coordinate points of the line.

Therefore, we'll need to find the slope of
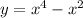`y=x^4-x^2` at the point where
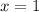`x=1` by taking its derivative and plugging
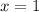`x=1` into the derivative:

`f(x)=x^4-x^2`

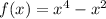
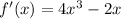`f'(x)=4x^3-2x` (Remember to use the Power Rule here!)

`f'(1)=4(1)^3-2(1)`

`f'(1)=4-2`

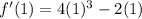
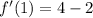
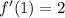`f'(1)=2` <-- Our slope here is 2

Now, evaluate
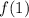`f(1)` to get
`y_1`:

`f(1)=1^4-1^2`

`f(1)=0`

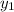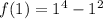
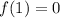
Therefore, the equation of the tangent line is:

`y-0=2(x-1)`

`y=2x-2`

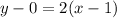
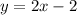
See attached graph for a visual reference