To evaluate the integral using the Gauss quadrature formula, we first need to express the integral as a definite integral over a finite interval. We can do this by making a substitution:
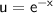 . The limits of integration will also change accordingly.
. The limits of integration will also change accordingly.
When
 ,
,
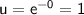 .
.
When
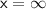 ,
,
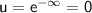 .
.
So the integral can be rewritten as:
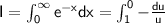
Now, we can apply the Gauss quadrature formula, which states that for the integral of a function
 over an interval
over an interval
![\sf [a, b]](https://img.qammunity.org/2024/formulas/mathematics/high-school/elpediyercguljap9no8zuuscs3d9t21xe.png) , we can approximate it using the weighted sum:
, we can approximate it using the weighted sum:
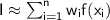
where
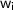 are the weights and
are the weights and
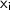 are the nodes.
are the nodes.
For our specific integral, we have
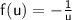 . We can use the Gauss-Laguerre quadrature formula, which is specifically designed for integrating functions of the form
. We can use the Gauss-Laguerre quadrature formula, which is specifically designed for integrating functions of the form
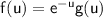 .
.
Using the Gauss-Laguerre weights and nodes, we have:
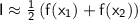
where
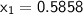 and
and
 .
.
Plugging in the function values and evaluating the expression, we get:
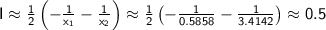
Therefore, the approximate value of the integral using the Gauss quadrature formula is
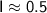 .
.

♥️
