Question

Saylin received $325 in gifts for her 8th Grade Moving Up Ceremony. She plans on investing all of it in an account earning 4.25% interest compounded annually. How much money will be in the account in four years?

A) $877.50

B) $383.87

C) $1340.12

D) $138.13

Answer 1

To calculate the future value of the investment, we can use the formula for compound interest:

`\sf A = P \left(1 + (r)/(n)\right)^(nt)`

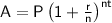
where:

`\sf A` = the future value of the investment

`\sf P` = the initial principal (amount invested)

`\sf r` = the interest rate (as a decimal)

`\sf n` = the number of times interest is compounded per year

`\sf t` = the number of years

In this case, Saylin received $325 and plans to invest it for 4 years at an interest rate of 4.25% compounded annually.

Substituting the values into the formula, we have:

`\sf A = 325 \left(1 + (0.0425)/(1)\right)^((1 * 4))`

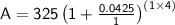
Simplifying the equation:

`\sf A = 325 * 1.0425^4`

Calculating the expression, we find:

`\sf A \approx 383.87`

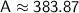
Therefore, the amount of money in the account after 4 years will be approximately $383.87. Thus, the correct option is B) 383.87.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`