Question

Solve using Gauss-Jordan elimination. 4x₁3x25x3 = 26 x₁ - 2x2 = 9 Select the correct choice below and fill in the answer box(es) within your choice. and X3 A. The unique solution is x₁ = x₂ = = B. The system has infinitely many solutions. The solution is x₁ (Simplify your answers. Type expressions using t as the variable.) x₂ = and x3 = t. = C. The system has infinitely many solutions. The solution is x₁, x₂ = s, and x3 = t. (Simplify your answer. Type an expression using s and t as the variables.) D. There is no solution.

Answer 1

`\huge\mathsf{ANSWER:}`

`\qquad\qquad\qquad`

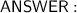
To solve using Gauss-Jordan elimination, we first need to write the system in augmented matrix form:

[4 3 25 | 26]

[1 -2 0 | 9]

We can perform row operations to get the matrix in row echelon form:

R2 → R2 - (1/4)R1

[4 3 25 | 26]

[0 -11 -25/4 | 5/2]

R2 → (-1/11)R2

[4 3 25 | 26]

[0 1 25/44 | -5/44]

R1 → R1 - 25R2

[4 0 375/44 | 641/44]

[0 1 25/44 | -5/44]

R1 → (1/4)R1

[1 0 375/176 | 641/176]

[0 1 25/44 | -5/44]

`\huge\mathsf{SOLUTION:}`

`\qquad\qquad\qquad`

This gives us the solution x₁ = 641/176 and x₂ = -5/44. However, we still have the variable x₃ in our original system, which has not been eliminated. This means that the system has infinitely many solutions. We can express the solutions in terms of x₃ as follows:

x₁ = 641/176 - (375/176)x₃

x₂ = -5/44 - (25/44)x₃

So the correct choice is (B) The system has infinitely many solutions. The solution is x₁ = 641/176 - (375/176)x₃, x₂ = -5/44 - (25/44)x₃, and x₃ can take on any value.