The function
 is defined as:
is defined as:
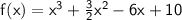
To find the stationary points of
 , we need to find the values of
, we need to find the values of
 where the derivative of
where the derivative of
 is equal to zero.
is equal to zero.
First, let's find the derivative of
 :
:

To find the stationary points, we set
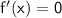 and solve for
and solve for
 :
:
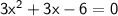
We can factor the quadratic equation as follows:
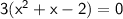
Now, we solve for
 by factoring further:
by factoring further:
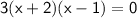
This gives us two solutions:
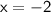 and
and
 .
.
So, the stationary points of
 are
are
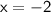 and
and
 .
.
To determine the intervals where
 is increasing, we need to analyze the sign of the derivative
is increasing, we need to analyze the sign of the derivative
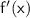 in different intervals. We can use the values of
in different intervals. We can use the values of
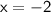 ,
,
 , and any other value between them.
, and any other value between them.
For
 , we choose
, we choose
 as a test point:
as a test point:
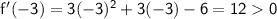
For
 , we choose
, we choose
 as a test point:
as a test point:

For
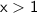 , we choose
, we choose
 as a test point:
as a test point:
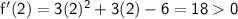
From the above analysis, we can conclude that
 is increasing in the intervals
is increasing in the intervals
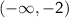 and
and
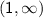 .
.
To find the inflection point of
 , we need to determine where the concavity changes. This occurs when the second derivative of
, we need to determine where the concavity changes. This occurs when the second derivative of
 changes sign.
changes sign.
The second derivative of
 is:
is:
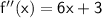
To find the inflection point, we set
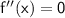 and solve for
and solve for
 :
:
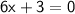
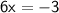
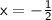
Therefore, the inflection point of
 is
is
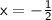 .
.