Question

Given sin A = sqr rt 41/ 4 and that angle A is in Quadrant I, find the exact value of sec⁡ A in simplest radical form using a rational denominator.

Answer 1

`\csc A = (√(41))/(5)`

Explanation:

To find the exact value of csc A in simplest radical form using a rational denominator, we can use the reciprocal identities of secant and cosecant:

`\boxed{\sec A = (1)/(\cos A)}\;\;\;\boxed{\text{csc} A = (1)/(\sin A)}`

Given sec A = √(41)/4, we can use the definition of secant as the reciprocal of cosine to find the value of cos A:

`\cos A=(1)/(\sec A)=(1)/((√(41))/(4))=(4)/(√(41))`

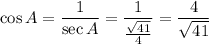
Since angle A is in Quadrant I, both sin A and cos A are positive.

Now we can substitute the value of cos A into the trigonometric identity to find sin A:

`\sin^2 A + \cos^2 A = 1`

`\sin^2 A + \left((4)/(√(41))\right)^2 = 1`

`\sin^2 A + (16)/(41) = 1`

`\sin^2 A = 1-(16)/(41)`

`\sin^2 A =(25)/(41)`

`\sin A=\sqrt{(25)/(41)}`

`\sin A=(5)/(√(41))`

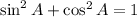
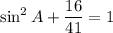
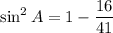
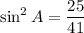
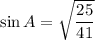
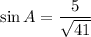
Finally, we can substitute the value of sin A into the reciprocal identity to find csc A:

`\text{csc} A = (1)/(\sin A) = (1)/((5)/(√(41))) = (√(41))/(5)`

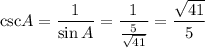
Therefore, the exact value of csc A in simplest radical form with a rational denominator is:

`\boxed{\csc A = (√(41))/(5)}`