Final Answer:
The partial derivatives of the function
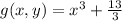 are
are
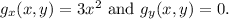 The critical point, where both partial derivatives are zero, is (0, 2).
The critical point, where both partial derivatives are zero, is (0, 2).
Step-by-step explanation:
Certainly, let's go through the detailed calculations step by step.
Given Information:
![\[ g(x, y) = x^3 + (13)/(3) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/uyndbfycumin04mdw57pauvmooyj7k2h44.png)
Partial Derivatives:
(a) To find the partial derivatives, differentiate
 with respect to
with respect to
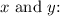
![\[ g_x(x, y) = (\partial g)/(\partial x) = 3x^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/t3afjwg4yjio685nn4i4zc6fsxnz7n3ouy.png)
![\[ g_y(x, y) = (\partial g)/(\partial y) = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/s4pn66q1db5omo52u0ecx7crpmtv7tmjbe.png)
(b) To find the critical points, set
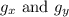 equal to zero and solve for
equal to zero and solve for
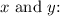
![\[ 3x^2 = 0 \implies x = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/nr436nfosec7a6uwn1kwu9w9sank4pguu9.png)
![\[ 2 - x = 0 \implies x = 2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/lcu3nvh99n8z1snu8ooizdmmmf166kcd0t.png)
Critical Point:
The critical point is where both partial derivatives are zero. Combining the solutions, we get
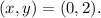
(a) The partial derivatives
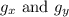 are obtained by differentiating
are obtained by differentiating
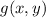 with respect to
with respect to
 respectively. The derivative of
respectively. The derivative of
 with respect to
with respect to
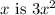 , and the constant term
, and the constant term
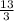 differentiates to zero. Therefore,
differentiates to zero. Therefore,
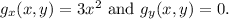
(b) To find the critical points, we set
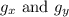 equal to zero. For
equal to zero. For
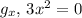 implies
implies
 results in
results in
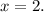 Combining these solutions, the critical point is
Combining these solutions, the critical point is
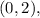 where both partial derivatives are zero.
where both partial derivatives are zero.
In summary, the partial derivatives
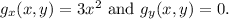 The critical point is
The critical point is
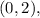 and these calculations provide a detailed understanding of the function's behavior and critical characteristics.
and these calculations provide a detailed understanding of the function's behavior and critical characteristics.