Answer:
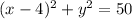
Explanation:
Given that the endpoints of the diameter of the circle are (3, -7) and (5, 7), we know that the center of these two points must represent the center of the circle. To determine this, we can use the midpoint formula to find the center,
 .
.
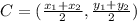

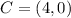
Now, with this in mind, we can figure out the radius,
 , of the circle. To do this, we can use the distance formula (or pythagorean theorem) from the center point
, of the circle. To do this, we can use the distance formula (or pythagorean theorem) from the center point
 to any of the two given endpoints, since we know the distance from either endpoint to the center is equal.
to any of the two given endpoints, since we know the distance from either endpoint to the center is equal.
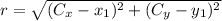 (
(
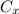 and
and
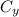 represent the x and y of the center, while
represent the x and y of the center, while
 and
and
 represent the x and y of either endpoint)
represent the x and y of either endpoint)
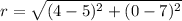 (Using point (5,7))
(Using point (5,7))
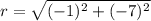
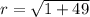

Knowing both the center,
 , and the radius,
, and the radius,
 , we can now write a formula for the circle. The formula for a circle is
, we can now write a formula for the circle. The formula for a circle is
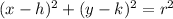 , where
, where
 represent the center, and
represent the center, and
 is the radius, as always.
is the radius, as always.
Finally, we get the equation:
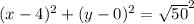
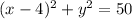
Below is a graph visualizing the circle and the 2 endpoints.