Answer:
(0, 4 +
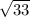 ) or approx. (0, 9.745)
) or approx. (0, 9.745)
AND
(0, 4 -
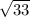 ) or approx. (0, -1.745)
) or approx. (0, -1.745)
Explanation:
Since you are attempting to look for all points on the y-axis that are 7 units away from (-4, 4), you can immediately assume that the x value of the coordinate must be 0.
Following this logic, we know that these points would be 4 units to the right, and x units up and down, to make a total distance of 7. To figure out x, you can use the pythagorean theorem:
 .
.
This gives us the equation:
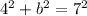
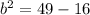
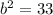
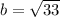
Now, we know there are 2 points on the y-axis that are a distance 7 away from the point (-4, 4). These points would be (0, 4 ±
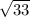 )
)
Therefore, all points on the y-axis 7 units from (-4, 4) would be:
1) (0, 4 +
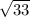 ) or approx. (0, 9.745)
) or approx. (0, 9.745)
2) (0, 4 -
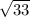 ) or approx. (0, -1.745)
) or approx. (0, -1.745)
An image is provided (where the red circle represents all points 7 away from (-4, 4), and the blue dots are the 2 points that we solved for above)