Question

Find x such that the distance between (5, -8) and (x, 4) is 13. (Enter your answers as a comma-separated list.) x= Need Help? Reed It

Answer 1

x = 10

Explanation:

We can find the distance, d, between two points using the distance formula, which is given by:

`d=\sqrt{(y_(2)-y_(1))^2+(x_(2)-x_(1))^2 }`, where

• (x1, y1) is one point,
• and (x2, y2) is another point.

Step 1: Plug in values for variables in the distance formula and simplify:

We can plug in 13 for d, (5, -8) for (x1, y1), and (x, 4) for (x2, y2) to find x

`13=√((4-(-8))^2+(x-5)^2)\\ 13=√((4+8)^2+(x-5)^2)\\ 13=√((12)^2+(x-5)^2)\\ 13=√(144+(x-5)^2)`

Step 2: Square both sides:

`13^2=(√(144+(x-5)^2))^2 \\169=144+(x-5)^2`

Step 3: Subtract 144 from both sides:

`(169=144+(x-5)^2)-144\\25=(x-5)^2`

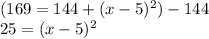
Step 4: Take the square root of both sides:

`√(25)=√((x-5)^2)\\ 5=x-5`

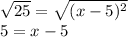
Step 5: Add 5 to both sides to find x:

`(5=x-5)+5\\10=x`

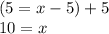
Thus, in order to have a distance of 13 between the (5, -8) and (x, 4), x must equal 10.

Optional Step 6: Plug in 10 for x in the distance formula and check that you get 13 on both sides of the equation when simplifying:

`13=√((4-(-8))^2+(10-5)^2)\\ 13=√((4+8)^2+(5)^2)\\ 13=√((12)^2+25)\\ 13=√(144+25)\\ 13=√(169)\\ 13=13`

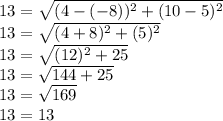
Thus, our answer is correct and x is 10.