Answer:
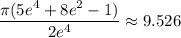
Explanation:
This can be solved with either the washer (easier) or the shell method (harder). For the disk/washer method, the slice is perpendicular to the axis of revolution, whereas, for the shell method, the slice is parallel to the axis of revolution. I'll show how to do it with both:
Shell Method (Horizontal Axis)
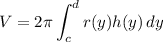
Radius:
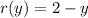 (distance from y=2 to x-axis)
(distance from y=2 to x-axis)
Height:
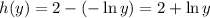 (
(
 is the same as
is the same as
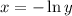 )
)
Bounds:
![[c,d]=[e^(-2),1]](https://img.qammunity.org/2024/formulas/mathematics/college/5d76gricgvfvxwbqja2w8whv60vozl1484.png) (plugging x-bounds in gets you this)
(plugging x-bounds in gets you this)
Plugging in our integral, we get:
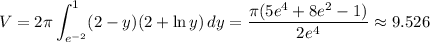
Washer Method (Parallel to x-axis)
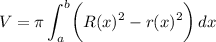
Outer Radius:
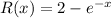 (distance between
(distance between
 and
and
 )
)
Inner Radius:
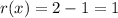 (distance between
(distance between
 and
and
 )
)
Bounds:
![[a,b]=[0,2]](https://img.qammunity.org/2024/formulas/mathematics/college/igfa9advgfaza853eqowiztldey77any66.png)
Plugging in our integral, we get:
![\displaystyle V=\pi\int^2_0\biggr((2-e^(-x))^2-1^2\biggr)\,dx\\\\V=\pi\int^2_0\biggr((4-4e^(-x)+e^(-2x))-1\biggr)\,dx\\\\V=\pi\int^2_0(3-4e^(-x)+e^(-2x))\,dx\\\\V=\pi\biggr(3x+4e^(-x)-(1)/(2)e^(-2x)\biggr)\biggr|^2_0\\\\V=\pi\biggr[\biggr(3(2)+4e^(-2)-(1)/(2)e^(-2(2))\biggr)-\biggr(3(0)+4e^(-0)-(1)/(2)e^(-2(0))\biggr)\biggr]\\\\V=\pi\biggr[\biggr(6+4e^(-2)-(1)/(2)e^(-4)\biggr)-\biggr(4-(1)/(2)\biggr)\biggr]](https://img.qammunity.org/2024/formulas/mathematics/college/r04kar29nlz7j9ib0c74xoijn7t7x6qh67.png)
![\displaystyle V=\pi\biggr[\biggr(6+4e^(-2)-(1)/(2)e^(-4)\biggr)-(7)/(2)\biggr]\\\\V=\pi\biggr((5)/(2)+4e^(-2)-(1)/(2)e^(-4)\biggr)\\\\V=\pi\biggr((5)/(2)+(4)/(e^2)-(1)/(2e^4)\biggr)\\\\V=\pi\biggr((5e^4)/(2e^4)+(8e^2)/(2e^4)-(1)/(2e^4)\biggr)\\\\V=\pi\biggr((5e^4+8e^2-1)/(2e^4)\biggr)\\\\V=(\pi(5e^4+8e^2-1))/(2e^4)\approx9.526](https://img.qammunity.org/2024/formulas/mathematics/college/1231pd8rrb1sc41poq8t3ls6hlg4r28slt.png)
Use your best judgment when deciding on what method you use when visualizing the solid, but I hope this helped!