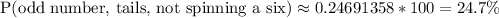Question

You spin the spinner, flip a coin, then spin the spinner again. Find the probability of the compound event. Write your answer as a fraction or percent rounded to the nearest tenth.

The probability of spinning an odd number, not flipping heads, then not spinning a 6 is

Answer 1

Answer: 24.7%

Explanation:

To find the probability of this compound event, we will first find the probability of each individual event.

`\displaystyle \text{P(odd number)}=\frac{\text{wanted outcome}}{\text{possible outcomes}}=\frac{\text{odd number}}{\text{parts of the spinner}}=(5)/(9) }`

`\displaystyle \text{P(not flipping heads)}=\frac{\text{wanted outcome}}{\text{possible outcomes}}=\frac{\text{flipping tails}}{\text{two sides to the coin}}=(1)/(2) }`

`\displaystyle \text{P(not spinning a six)}=\frac{\text{wanted outcome}}{\text{possible outcomes}}=\frac{\text{1, 2, 3, 4, 5, 7, 8, 9}}{\text{parts of the spinner}}=(8)/(9) }`

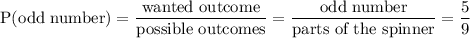
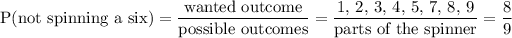
Next, we will multiply all of these event probabilities together to find the compound event.

`\displaystyle \text{P(odd number, tails, not spinning a six)}=(5)/(9)*(1)/(2)*(8)/(9)=(40)/(162)=(20)/(81) \approx 0.24691358`

Lastly, we will take this value and multiply it by 100 to create a percentage. Then we will round to the nearest tenth.

`\displaystyle \text{P(odd number, tails, not spinning a six)} \approx 0.24691358 * 100 = 24.7\%`