Question

Word problem using derivatives. Please see attached picture, 30 points.

Answer 1

`{(dx)/(dt) \approx-1051 \ ft/s`

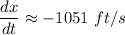
Explanation:

To find the rate at which the shadow of the skydiver is moving along the ground, we need to determine the horizontal distance traveled by the skydiver's shadow over time.

Given that the angle of elevation to the sun from the ground is 50°, we can consider the shadow of the skydiver as a right triangle formed by the height of the skydiver, h(t), and the horizontal distance traveled by the shadow, x(t).

We can find the horizontal distance using the trigonometric relationship between the angle and the sides of the triangle.

`\tan(50\°) = (h(t))/(x(t))\\\\\\\Longrightarrow \boxed{x(t)=(h(t))/(\tan(50\°))}`

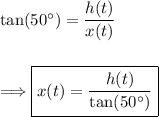
h(t) is given as, h(t)=-16t²+25000. Plugging this in we have:

`x(t)=(h(t))/(\tan(50\°))\\\\\\\\\Longrightarrow x(t)=(-16t^2+25000)/(\tan(50\°))`

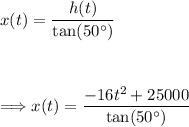
To find the rate at which the shadow is moving along the ground, we differentiate x(t) with respect to time, t.

Using the quotient rule:

`\boxed{\left\begin{array}{ccc}\text{\underline{The Quotient Rule:}}\\\\(d)/(dx)\Big[(f(x))/(g(x)) \Big] = (f'(x)g(x)-f(x)g'(x))/((g(x))^2)\end{array}\right }`

`\Longrightarrow x'(t)=(((d)/(dx) [-16t^2+25000])(\tan(50\°))-(-16t^2+25000)((d)/(dx)[\tan(50\°)]) ))/((\tan(50\°))^2)\\\\\\\\\Longrightarrow x'(t)=((-32t)(\tan(50\°))-(-16t^2+25000)(0) )/((\tan(50\°))^2)\\\\\\\\\Longrightarrow x'(t)=((-32t)(\tan(50\°))+0 )/((\tan(50\°))^2)\\\\\\\\\therefore \boxed{x'(t)=(-32t)/(\tan(50\textdegree)) }`

Now find the time when the height is 500 ft.

`h(t)=-16t^2+25000; \ h(t)=500\\\\\\\Longrightarrow 500=-16t^2+25000\\\\\\\Longrightarrow -24500=-16t^2\\\\\\\Longrightarrow t^2=(6125)/(4)\\\\\\\therefore \boxed{t=(35\sqrt5)/(2) \ s}`

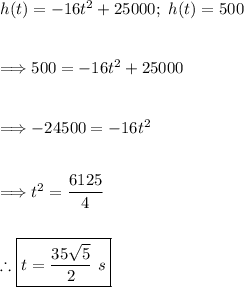
Using the value we just found for time, plug this in for t.

`x'(t)=(-32t)/(\tan(50\textdegree)) \\\\\\\\\Longrightarrow x'(t)=(-32\Big((35\sqrt5)/(2) \Big))/(\tan(50\textdegree)) \\\\\\\\\therefore \boxed{\boxed{x'(t)=(dx)/(dt) \approx -1051 \ ft/s}}`

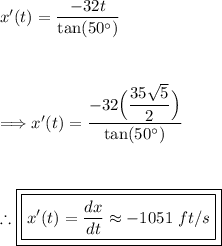
Thus, the problem is solved. Note that the question may have you disregard the negative.