Question

Calc II Question

The base of s is an elliptical region with boundary curve 9x^2 + 4y^2 = 36
Cross sections perpendicular to the x axis are isoscelees right triangle with hypotension in the base.


Correct answer is 24 but I don't know how they go that

Answer 1

See below for explanation

Explanation:

The area of an isosceles triangle is
`A=(1)/(2)bh`, so let's write the base as an equation of y:

`\displaystyle 9x^2+4y^2=36\\\\4y^2=36-9x^2\\\\y^2=9-(9)/(4)x^2\\\\y=\pm\sqrt{9-(9)/(4)x^2`

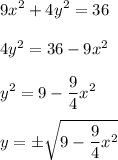
As you can see, our ellipse consists of two parts, so the hypotenuse of each cross-section will be
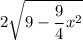`\displaystyle 2\sqrt{9-(9)/(4)x^2`, and each height will be
`\displaystyle \sqrt{9-(9)/(4)x^2}`.

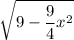Hence, the area function for our cross-sections are:

`\displaystyle A(x)=(1)/(2)bh=(1)/(2)\cdot2\sqrt{9-(9)/(4)x^2}\cdot\sqrt{9-(9)/(4)x^2}=9-(9)/(4)x^2`

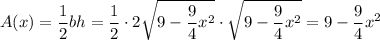
Since we'll be integrating with respect to x because the cross-sections are perpendicular to the x-axis, then our bounds will be from -2 to 2 to find the volume:

`\displaystyle V=\int^2_(-2)\biggr(9-(9)/(4)x^2\biggr)\,dx\\\\V=9x-(3)/(4)x^3\biggr|^2_(-2)\\\\V=\biggr(9(2)-(3)/(4)(2)^3\biggr)-\biggr(9(-2)-(3)/(4)(-2)^3\biggr)\\\\V=\biggr(18-(3)/(4)(8)\biggr)-\biggr(-18-(3)/(4)(-8)\biggr)\\\\V=(18-6)-(-18+6)\\\\V=12-(-12)\\\\V=12+12\\\\V=24`

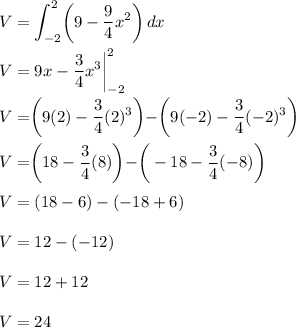
Therefore, this explanation confirms that the correct volume is 24!